[AI] 인공지능을 위한 기초 수학

인공지능 공부를 위한 수학 지식 학습 후 정리한 포스팅 입니다.

부족한 지식을 틈틈이 추가하겠습니다.

- 2023.03.11 시작

인공지능은 수학이 전부다.,;;;

 

 

 

 

 

1) MLE

ref: https://angeloyeo.github.io/2020/07/17/MLE.html

최대우도법(MLE) - 공돌이의 수학정리노트

https://process-mining.tistory.com/93

Maximum Likelihood란? (MLE란?)

최대우도법 : 어떤 평균값을 갖는 확률밀도로 부터 이 샘플들이 추출되었을까?????

 

likelihood (가능도, 우도): 추출된 데이터가 분포로 부터 나왔을 가능도

주어진 파라미터 분포에 대해 샘플의 데이터가 얼마나 그럴 듯 한지 계산한 값

조건부 확률 값은 맞지만 합이 1이 아니므로 확률 분포는 아니다. (prior 고정, posterior를 함수로)

사전 확률은 보고 그 속에 숨어 있는 사후확률을 찾고자 함 ( |는 마치 벽처럼 작용)

 

θ가 뭐였길래 Xn이 이렇게 나왔을까? 에 대한 답을 하고 싶은 것 

likelihood는 θ에 대해서 measurement가 Xn으로 나올 그 확률 밀도 값이므로 likelhood가 최대가 되는 x가 바로 내가 찾고자하는 θ이다.

각 데이터 샘플에서 후보 분포에 대한 높이 (likelihood)를 계산해서 곱한 것의 합을 통해 계산이 가능하다.

분포가 정규 분포의 파라미터를 갖고 있는 정규분포라고 가정하면 데이터가 정규분포를 따를 확률은 다음과 같다.(단, P(Xn)은 사전 확률, P(Xn | θ)는 사후 확률

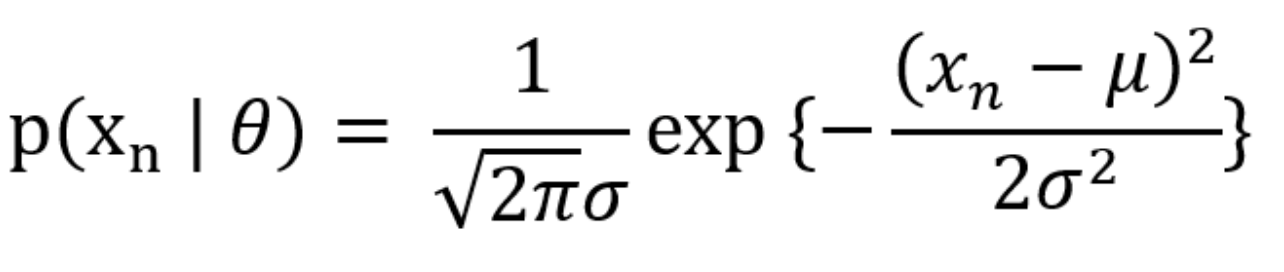
모든 데이터가 독립적이라고 가정하면 독립의 곱셈 정리에 의해 다음과 같다.

즉 likelihood function은 다음과 같다.

 

 

 

likelihood function을 자연로그를 취해 log-likelihood function으로 표현하면 다음과 같다.

log함수는 단조 증가 함수로 likelihood 함수의 최대값이 발생하는 정의역은 log-likelihood function의 최대값이 발생하는 정의역과 같다.

찾고자 하는 파라미터에 대해 편미분 하여 likelihood function의 최대값을 찾을 수 있다.

 

(log를 취하는 이유는 이진분류의 loss function에서 log를 취해주는 것과 비슷한 이유이지 않을까.,?)

2) 

3) 

4) 

 

 

*유의사항

- 인공지능공학과 학부생이 공부하여 남긴 정리입니다.

- 정확하지 않거나, 틀린 점이 있다면 댓글로 알려주시면 감사하겠습니다.