[선형대수학] 선형방정식과 선형시스템

이번 포스팅에서는 선형방정식과 선형시스템의 개념을 구체적인 예시와 함께 학습합니다.
그리고, 선형방정식의 해를 구하기 위한 방법 중 역행렬과 항등 행렬의 개념에대해 학습합니다.

핵심 키워드

• 선형방정식
• 선형시스템
• 항등행렬
• 역행렬

I) 선형방정식

변수들 사이의 관계가 직선적인 관계나 혹은 비례관계를 나타내는 일차함수식을 말한다.

변수 $x_{1},x_{2},\cdots,x_{n}$ , 상수 b, 계수 $a_{1},a_{2},\cdots,a_{n}$ 에 대해 선형방정식은 다음과 같다.

$\large a_{1}x_{1}+a_{2}x_{2}+\cdots+a_{n}x_{n}= b$

위의 식은 다음과 같이 적을 수 있다.

$\large a=\begin{bmatrix} a_{1} \\ a_{2} \\ \vdots \\ a_{n} \end{bmatrix}$ 이고, $\large x=\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix}$ 이면 $\textbf{a}^{\textit{T}}\mathbf{x} = b$ 이다.

II) 선형시스템

선형방정식의 집합을 선형시스템이라고 한다. 하나 혹은 그 이상의 선형 방정식이 같은 변수를 포함하고 있을 때 선형시스템이라고 한다.

1. 선형시스템의 예시

주당 음주횟수, 흡연 여부, 숙면 시간, 기대수명 데이터를 수집했다고 가정하자.

Person ID	Number of drinks per week	Smoking	Sleep time	Life-span
1	1	No (=0)	360 minutes	80
2	3	Yes (=1)	420 minutes	75
3	5	Yes (=1)	400 minutes	72

우리는 다음과 같은 선형 시스템을 세울 수 있다.

$\large1x_{1}+0x_{2}+360x_{3} = 80$
$\large3x_{1}+1x_{2}+420x_{3} = 75$
$\large5x_{1}+1x_{2}+400x_{3} = 72$

우리는 주어진 변수를 구할 수 있다면 주당 음주횟수, 흡연 여부, 숙면 시간를 통해 기대수명을 예측할 수 있다.
이제, 선형시스템을 행렬을 이용해 풀어보자.

$ \large A=\begin{bmatrix} 1 & 0 & 360 \\ 3 & 1 & 420 \\ 5 & 1 & 400\\ \end{bmatrix} $ $ \large\textbf{x}=\begin{bmatrix} x_{1}\\ x_{2} \\ x_{3} \end{bmatrix} $ $\large b=\begin{bmatrix} 80 \\ 75 \\ 72 \end{bmatrix} $

위와 같이 계수, 변수, 타겟값을 표현할 수 있고, 이제 A x = b 를 만족하는 x를 구하면된다.
이제, 선형방정식의 해를 구하기 위해 항등행렬과 역행렬에 대해 학습해보자.

III) 항등행렬

주대각선의 모든 성분은 1이고 나머지 성분은 0인 정사각행렬이다. 곱셈에 대해 항등원이 되므로 단위행렬이라고도 부른다.

$ \large A=\begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{bmatrix} $

IV) 역행렬

두개의 정사각행렬 $ A \in \mathbb{R}^{n\times n}$ 와 $ A^{-1} $, 항등행렬 I에 대해

$ \large AA^{-1} = A^{-1}A = I $

을 만족하면 $ A^{-1} $ 를 A의 역행렬이라고 한다.

● 역행렬은 정사각행렬(정방행렬)에서만 존재한다. $AA^{-1} = A^{-1}A = I$ 을 만족하는 직사각행렬은 역행렬이 아니다.
● 2 X 2 행렬에서 역행렬을 구하는 간단한 식

2 X 2 행렬에서 역행렬을 구하는 간단한 식

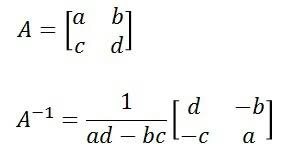
이제 예제의 선형시스템에서 x를 구해보자.

$ \large A^{-1} = \begin{bmatrix} 0.027 & -0.486 & 0.486 \\ -1.22 & 1.89 & -0.892\\ 0.0027& 0.00135 & -0.00135 \\ \end{bmatrix} $

$ \large x = A^{-1}b = \begin{bmatrix} 0.027 & -0.486 & 0.486 \\ -1.22 & 1.89 & -0.892\\ 0.0027& 0.00135 & -0.00135 \\ \end{bmatrix} \begin{bmatrix} 80 \\ 75 \\72 \end{bmatrix}= \begin{bmatrix} 0.703 \\ -19.6 \\ 0.220 \end{bmatrix}$

이렇게 행렬을 통해 가중치를 구할 수 있다.
우리가 구하려는 기대수명식은 아래와 같다.

(기대 수명) = 0.703 X (주당 음주 횟수) + -19.6 X (흡연 유무) + 0.220 X (숙면 시간)

역행렬이 존재한다면 Ax = b 를 만족하는 x는 오직 하나이다.
역행렬의 존재를 파악하기 위해서는 행렬 A에 대해 det A = 0 임을 확인하면 된다.
determinant를 구하는 자세한 방법은 아래 링크를 통해 확인이 가능하다.
determinant구하기1

Lecture 18: Properties of determinants | Video Lectures | Linear Algebra | Mathematics | MIT OpenCourseWare

determinant구하기2

Lecture 19: Determinant formulas and cofactors | Video Lectures | Linear Algebra | Mathematics | MIT OpenCourseWare

+) 직사각행렬의 선형방정식

Person ID	Number of drinks per week	Smoking	Sleep time	Life-span
1	1	No (=0)	360 minutes	80
2	3	Yes (=1)	420 minutes	75
3	5	Yes (=1)	400 minutes	72

위 그래프에서 Person ID의 수를 m, 주당 음주 횟수, 흡연 유무, 숙면 시간 등의 변수를 n 이라고 하면
m < n 일때, 변수가 방정식 보다 많기 때문에 해가 무한히 발생한다.
m > n 일때, 방정식이 변수 보다 많기 때문에 해가 존재하지 않는다.
이때 해결법 추후 포스팅에서 다루어 보겠습니다.

감사합니다 :)